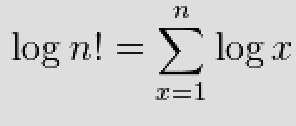- Mark as New
- Bookmark Message
- Subscribe to Message
- Mute Message
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark Message
- Subscribe to Message
- Mute Message
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
You could try an approximation by using the natural logarithm (see formula in picture below).
That should work fine when n is not too big, if n is big enough you might have approximation errors. Using the Stirling's approximation is more accurate in this case but it won't be easy to implement with the Splunk built-in commands.
See an example below for the natural logarithm approximation when n=5:
| stats count
| fields - count
| eval n = 5
| eval ki = mvrange(1, n+1)
| mvexpand ki
| eval ln_ki = ln(ki)
| eventstats sum(ln_ki) as sum_ln_ki by n
| eval n_factorial = round(exp(sum_ln_ki))
| stats first(n_factorial) as n_factorial by n
Alternative that performs the exponential calculations at the end and might improve performance. Give it a go too:
| stats count
| fields - count
| eval n = 5
| eval ki = mvrange(1, n+1)
| mvexpand ki
| eval ln_ki = ln(ki)
| eventstats sum(ln_ki) as sum_ln_ki by n
| stats count by n, sum_ln_ki
| eval n_factorial = round(exp(sum_ln_ki))
| fields - count, sum_ln_ki
- Mark as New
- Bookmark Message
- Subscribe to Message
- Mute Message
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
You could try the App for R. It doesn't seem to be on Splunkbase any more, but it's apparently available from a link the_wolverine supplies in this answer for what happened to the R project. To help prevent double-hopping, here's the link they supplied: https://github.com/rfsp/r
- Mark as New
- Bookmark Message
- Subscribe to Message
- Mute Message
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
You could try an approximation by using the natural logarithm (see formula in picture below).
That should work fine when n is not too big, if n is big enough you might have approximation errors. Using the Stirling's approximation is more accurate in this case but it won't be easy to implement with the Splunk built-in commands.
See an example below for the natural logarithm approximation when n=5:
| stats count
| fields - count
| eval n = 5
| eval ki = mvrange(1, n+1)
| mvexpand ki
| eval ln_ki = ln(ki)
| eventstats sum(ln_ki) as sum_ln_ki by n
| eval n_factorial = round(exp(sum_ln_ki))
| stats first(n_factorial) as n_factorial by n
Alternative that performs the exponential calculations at the end and might improve performance. Give it a go too:
| stats count
| fields - count
| eval n = 5
| eval ki = mvrange(1, n+1)
| mvexpand ki
| eval ln_ki = ln(ki)
| eventstats sum(ln_ki) as sum_ln_ki by n
| stats count by n, sum_ln_ki
| eval n_factorial = round(exp(sum_ln_ki))
| fields - count, sum_ln_ki
- Mark as New
- Bookmark Message
- Subscribe to Message
- Mute Message
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Here's Stirling's Approximation in SPL: `| eval n! = sqrt(2*pi()*n)*pow(n/exp(1), n)`
- Mark as New
- Bookmark Message
- Subscribe to Message
- Mute Message
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
By the way, if you find a different answer that works for you please post it here so that others can benefit from it.
- Mark as New
- Bookmark Message
- Subscribe to Message
- Mute Message
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hey thanks ! and sorry for late reply. Yes it did work for me. Also custom command option seems to be good
- Mark as New
- Bookmark Message
- Subscribe to Message
- Mute Message
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
The splunk eval functions dont offer factorial computator.
You could create a custom command & offload the factorial generation logic to the python code.
http://docs.splunk.com/Documentation/Splunk/6.2.3/AdvancedDev/Searchscripts
- Mark as New
- Bookmark Message
- Subscribe to Message
- Mute Message
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
You can use a lookup table. Precompute as many factorials as you think you may need (probably not many, considering how quickly they grow) and then look them up as you need.