Are you a member of the Splunk Community?
- Find Answers
- :
- Apps & Add-ons
- :
- All Apps and Add-ons
- :
- Why is the PACF out of limits in the Splunk Machin...
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark Topic
- Subscribe to Topic
- Mute Topic
- Printer Friendly Page
- Mark as New
- Bookmark Message
- Subscribe to Message
- Mute Message
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Why is the PACF out of limits in the Splunk Machine Learning Toolkit?
Hello all, during the development of a project, we faced some problems concerning the Partial Autocorrelation Function (PACF), when using the Splunk Machine Learning Toolkit version 3.1.0.
Theoretically, the PACF gives us values in the range -1 to 1 and allows us to analyze the dependence and behavior between different lags.
If we run the default function, we obtained some lags for which the observed absolute PACF value was greater than 1.

We thought it could be the case that for huge lags, some error occurred. But we also obtained a similar trouble for lags < 50.

Then we decided to specify the method that we use to calculate it – Yule-Walker with or without bias correction, Ordinary Least Squares, Levison-Durbin with or without bias correction. For some of them we got once again lags for which the absolute PACF value was greater than 1, but fortunately, we also obtained decent values – especially using OLS method.
Does anyone has experienced similar results or knows what is the reason for them to happen?
We suspect that it might be caused by error accumulation since all methods mentioned are numerical methods that suppose some type of convergence.
(Also – funny fact – if one checks the manual, it will see in the description of the PACF function a plot where PACF takes a maximum absolute value of almost 6 (?), which is theoretically impossible. Here is the link:
https://docs.splunk.com/Documentation/MLApp/3.1.0/User/ForecastTimeSeries#PACF_Residual:_partial_aut... )
- Mark as New
- Bookmark Message
- Subscribe to Message
- Mute Message
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi @diasna1,
Does anyone has experienced similar results or knows what is the reason for them to happen?
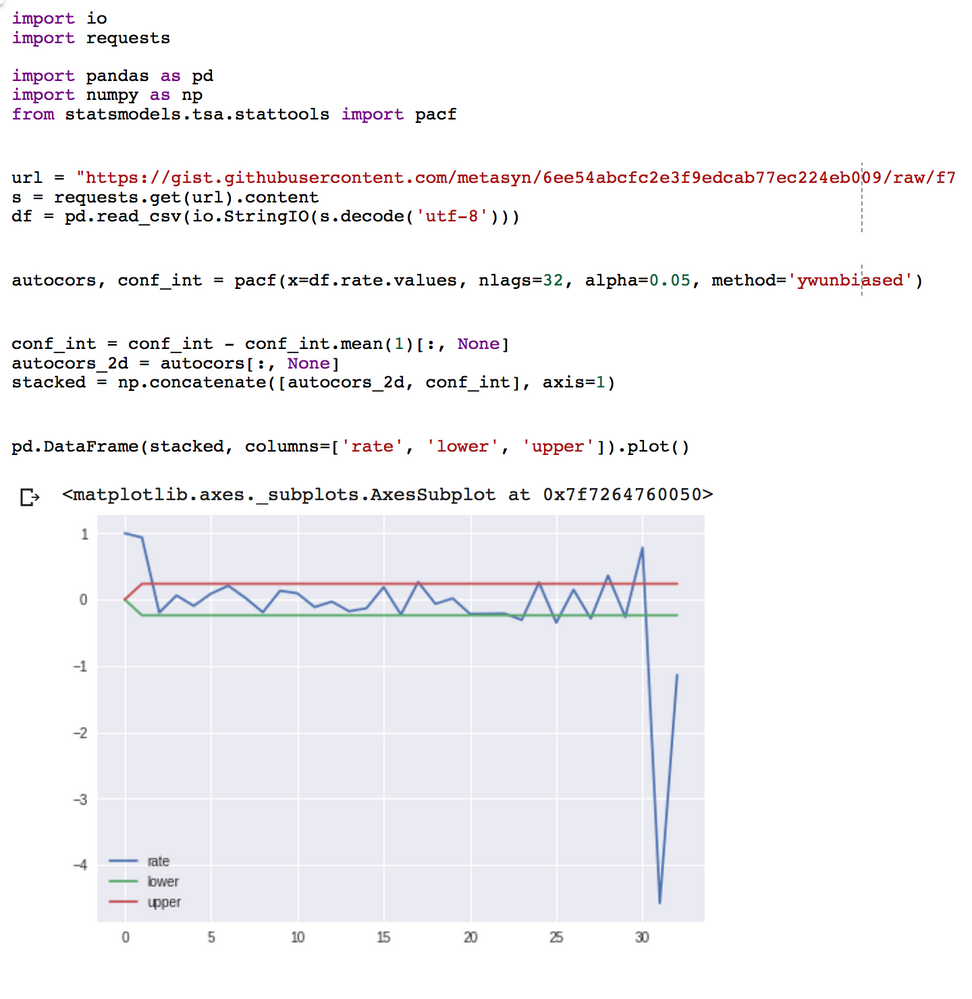
These large PACF values can be repeated - here's a pure python example:
In the example above (and the same dataset used in the part of the documentation you reference) you'll notice that the PACF values start going outside of the -1 to 1 range when get past 1/2 the size of the dataset. Put simply, we're reaching the limits of a valid lag value.
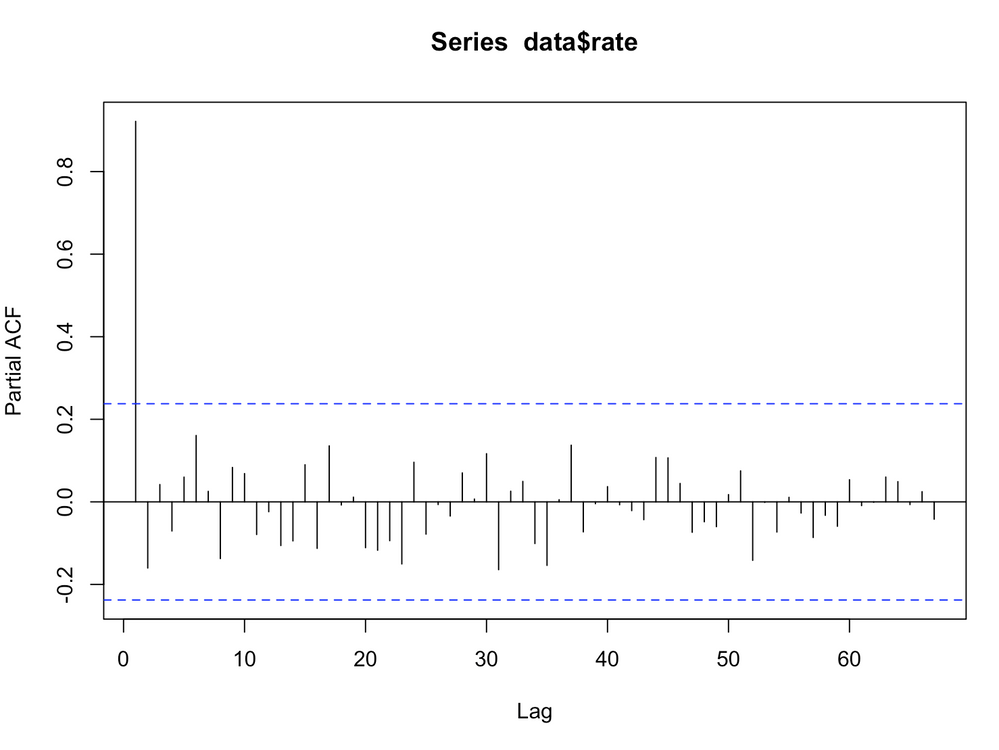
You'll notice in the screenshot you posted, it happens around the 1/2 mark as well. Interestingly, this doesn't happen when you run the same partial autocorrelation in R:
data = read.csv('/opt/splunk/etc/apps/Splunk_ML_Toolkit/lookups/exchange.csv')
pacf(data$rate, lag.max=100)
which gives us:
So, why do they differ?
You may appreciate reading this post about a similar discrepancy between the partial correlation implementation used in Matlab:
https://www.mathworks.com/matlabcentral/answers/122337-wrong-function-partial-autocorrelation-pacf-p...
The statsmodels version (which is what is used in the MLTK), as you mention, has a number of different methods used for calculating the actual correlations, some of which give different results.
The R implemetation of pacf also uses yule-walker:
The partial autocorrelations are obtained from Yule-Walker estimates of the successive autoregressive processes. The algorithm of Durbin is used (see Box and Jenkins (1976), p. 65).
Here are the two implementations, if you want to try to disambiguate them:
R: https://github.com/wch/r-source/blob/45179ea9ed1015b11e553eb8cd2b7eef0e3adf8a/src/library/stats/R/ar...
Statsmodels: http://www.statsmodels.org/dev/_modules/statsmodels/regression/linear_model.html#yule_walker
Anyhow, I hope that answers your question: that the differences stem from their underlying implementations. Its interesting too, that stationarity assumptions might not be met. For the example above...
In R:
library("tseries")
adf.test(data$rate)
.
Augmented Dickey-Fuller Test
.
data: data$rate
Dickey-Fuller = -2.0704, Lag order = 4, p-value = 0.5466
alternative hypothesis: stationary
We can see that we're far from rejecting the null or accepting the alternative, at least for this dataset.
Feel free to continue the conversation on the Splunk slack usergroup workspace (http://splk.it/slack) on the #machinlearning channel - I'm @alexanderjohnson there.