Are you a member of the Splunk Community?
- Find Answers
- :
- Using Splunk
- :
- Splunk Search
- :
- Predict - 95% Confidence Interval
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark Topic
- Subscribe to Topic
- Mute Topic
- Printer Friendly Page
- Mark as New
- Bookmark Message
- Subscribe to Message
- Mute Message
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I have read through Splunk docs that Splunk defaults lower and upper Confidence Interval to 95% for its prediction using predict command. I am trying to understand further its interpretation (i.e. what Confidence Interval means to my dashboard). Technically, please help advise as to why is it defaulted at 95% rather than any other percentages? and also of its computation if possible?
Responses are highly appreciated. Thank you!
- Mark as New
- Bookmark Message
- Subscribe to Message
- Mute Message
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi, arielpconsolacion.
This is all about statistics. 95% is two standard deviations, a very common "threshold" used in statistics and the sciences for "if something's very likely."
The beginning and "simple examples" section of the wikipedia article for standard deviation help a little. There's a linked article on the 68-95-99.7 rule which also has some decent information in it too.
A simplified and vague example may help.
Let's assume you are counting network events. (The actual thing you are counting or measuring doesn't really matter). If you have over the past 6 hours a pretty consistent measurement, let's say right around 100 events per minute (Like, 98, 102, 100,101, 99, 106, 100, 99, 97, 98 ... essentially hovering close to 100) , then you have a couple of things you can say.
You could say the most likely individual measurement you would expect 5 minutes from now is 100. But you would be hard pressed to say it WILL be 100, right? Just that it's likely close.
Well, if you did all the math to find your standard deviation (I don't suggest it except in the simplest of examples), and you found that standard deviation to be 5, then you could say it's probably likely 5 minutes from now your expected measurement will be between 95 and 105 (100 +/- 5). That's your one standard deviation, where 68% of the time you'd expect the actual value you measure (when you get 5 minutes later) to within your "prediction".
Now, here's the key one: if you wanted to know the prediction for the span of your measurement in 5 minutes that should cover the expected value 95 times out of 100, you double your standard deviation and you get the "default" 95% threshold. So, in our example, 95% of the time you'd expect the actual measurement in 5 minutes to be between 90 and 110.
Here's the thing about the standard deviation in this example. We pretended to use pretty consistent initial numbers so our standard deviation is pretty low. If instead you have more varying initial numbers, like 102, 156, 99, 64, 45, 150, 155, 100...., then perhaps our "average" is still pretty close to 100 (I don't know, I didn't actually do the math!). But the standard deviation will be far greater, perhaps +/- 50. Which means your predictions will be all over the place. In that case, the "range" of actual values the count could take on 5 minutes from now is BIG. It's hard to predict. You'll still get a prediction, but it's more vague and has less "predictive value" because of all that variation, so the range will be bigger.
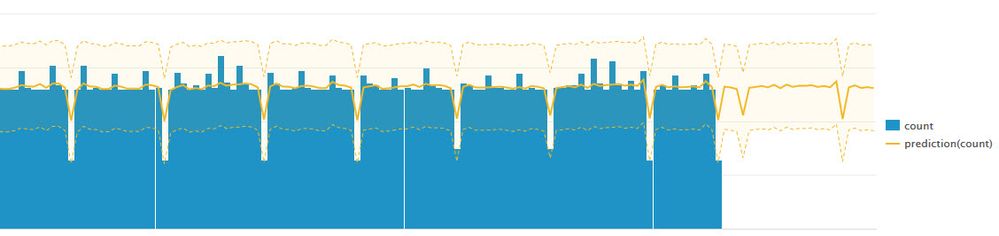
Here's an example of data that's pretty predictable:
You'll see that it's consistent and there's quite a bit of it. The more data points you have the better your prediction capability, right?
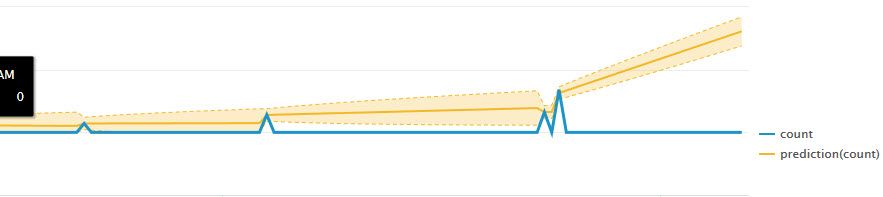
Here's an example of data that's so sparse it's hard to predict.
There's just so little the "predict" command can't do anything accurate with it. That's similar to having data, but it being so scattered that it's hard to predict.
In general, if you don't have 30+ data points your predictions will be poor. If you have high variation (that doesn't have a nice, easily discerned repeating pattern), your predictions will also be poor. Like the second example.
If instead you have fairly large amount of consistent (or consistently changing) data the predictions can be pretty tight. Like the first example.
- Mark as New
- Bookmark Message
- Subscribe to Message
- Mute Message
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi, arielpconsolacion.
This is all about statistics. 95% is two standard deviations, a very common "threshold" used in statistics and the sciences for "if something's very likely."
The beginning and "simple examples" section of the wikipedia article for standard deviation help a little. There's a linked article on the 68-95-99.7 rule which also has some decent information in it too.
A simplified and vague example may help.
Let's assume you are counting network events. (The actual thing you are counting or measuring doesn't really matter). If you have over the past 6 hours a pretty consistent measurement, let's say right around 100 events per minute (Like, 98, 102, 100,101, 99, 106, 100, 99, 97, 98 ... essentially hovering close to 100) , then you have a couple of things you can say.
You could say the most likely individual measurement you would expect 5 minutes from now is 100. But you would be hard pressed to say it WILL be 100, right? Just that it's likely close.
Well, if you did all the math to find your standard deviation (I don't suggest it except in the simplest of examples), and you found that standard deviation to be 5, then you could say it's probably likely 5 minutes from now your expected measurement will be between 95 and 105 (100 +/- 5). That's your one standard deviation, where 68% of the time you'd expect the actual value you measure (when you get 5 minutes later) to within your "prediction".
Now, here's the key one: if you wanted to know the prediction for the span of your measurement in 5 minutes that should cover the expected value 95 times out of 100, you double your standard deviation and you get the "default" 95% threshold. So, in our example, 95% of the time you'd expect the actual measurement in 5 minutes to be between 90 and 110.
Here's the thing about the standard deviation in this example. We pretended to use pretty consistent initial numbers so our standard deviation is pretty low. If instead you have more varying initial numbers, like 102, 156, 99, 64, 45, 150, 155, 100...., then perhaps our "average" is still pretty close to 100 (I don't know, I didn't actually do the math!). But the standard deviation will be far greater, perhaps +/- 50. Which means your predictions will be all over the place. In that case, the "range" of actual values the count could take on 5 minutes from now is BIG. It's hard to predict. You'll still get a prediction, but it's more vague and has less "predictive value" because of all that variation, so the range will be bigger.
Here's an example of data that's pretty predictable:
You'll see that it's consistent and there's quite a bit of it. The more data points you have the better your prediction capability, right?
Here's an example of data that's so sparse it's hard to predict.
There's just so little the "predict" command can't do anything accurate with it. That's similar to having data, but it being so scattered that it's hard to predict.
In general, if you don't have 30+ data points your predictions will be poor. If you have high variation (that doesn't have a nice, easily discerned repeating pattern), your predictions will also be poor. Like the second example.
If instead you have fairly large amount of consistent (or consistently changing) data the predictions can be pretty tight. Like the first example.
- Mark as New
- Bookmark Message
- Subscribe to Message
- Mute Message
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thank you for responding rich7177. Appreciated.
For the 95% defaulted Confidence Interval, I understand that values lower than 95 would mean a lower probability that the actual value would fall in the Confidence Interval from the Splunk's prediction. right? But why isn't 100% used instead?
- Mark as New
- Bookmark Message
- Subscribe to Message
- Mute Message
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Right on the first part, lower values than 95 means there's a lower likelihood the actual value, when you finally measure it, will be within that range.
Let's talk a bit about the 100% confidence interval. What would that say? "I can say with 100% confidence that the next value of this sequence of numbers will be between X and Y." What would you pick for X and Y to get that 100% confidence interval? Not really, really likely to be, but actually "WILL BE" within that range, even if I have broken equipment or the Russians invade Poland or ... or ...?
For a count such as we we using as an example, I could only pick X to be zero (counts can't be negative) and Y to be positive infinity. You'd have to pick such a large range because a 100% confidence interval is a guarantee that the next, unknown value will fall between X and Y. Regardless of what this particular sequence did in the past, you really are only guessing what it'll do next time and if you had to make a guarantee...
Now, in real life it won't be positive infinity, for sure. In my case pretend case (the first one, with the fairly consistent data about 100) you may know that the equipment isn't rated to handle more than 10,000 events per minute. In that case you could "kind of" say you had a 100% confidence interval of zero to 20,000 (because you never know and vendors lie). But still, I'm sure you get the point that it's not really very helpful because it has to cover every possible value that measurement could take.
So 100% is not achievable. Or maybe a better way to describe is is 100% is achievable but tells you nothing. You can get fairly close on some data, but real life data is usually more messy.
Compare that sort of guarantee to "75% of the time the value will fall between 98 and 103". Or "95% of the time the value will fall between 93 and 108". Or even "I'm nearly certain - 99.9% confident - that the next value will fall between 60 and 141."
How's the old joke go? The only things you can say will happen with 100% certainty are death and taxes. 🙂